1 Kinetics 1.5 Change of variables and solid angles 2 The first law

1.6 Pressure and effusion

(September 1, 2023)

After a change of variables the probability distribution of velocities $(v_{x},v_{y},v_{z})$ can be written as distribution particles with the speed $v$ , flying with angles $\theta$ and $\phi$ :

$\displaystyle{\rm d}\mathscr{P}_{v,\theta,\phi}=$	$\displaystyle\left(\frac{m}{2\pi{kT}}\right)^{3/2}e^{-mv^{2}/2{k_{% \scriptscriptstyle B}T}}\;v^{2}\sin\theta\;{\rm d}v{\rm d}\theta{\rm d}\phi$	(1.71)
$\displaystyle=$	$\displaystyle\left(\frac{m}{2\pi{kT}}\right)^{3/2}e^{-mv^{2}/2{k_{% \scriptscriptstyle B}T}}4\pi v^{2}{\rm d}v\;\frac{\sin\theta{\rm d}\theta{\rm d% }\phi}{4\pi}$	(1.72)
$\displaystyle=$	$\displaystyle P(v){\rm d}v\,\frac{{\rm d}\Omega}{4\pi}$	(1.73)

where we have recalled Eq. (1.53) for the speed distribution. Thus, the probability of $v,\theta,\phi$ in a specified range is probability of speed $v$ in a range $d v$ , times a probability of angles which are uniformly distributed the sphere, i.e. ${\rm d}\mathscr{P}_{\Omega}/{{\rm d}\Omega}=1/4\pi$ . The number of particles per volume with speed in $[v,v+dv]$ and angles in $[\theta,\theta+{\rm d}\theta]$ and $[\phi,\phi+{\rm d}\phi]$ is given by the probability in Eq. (1.73) multiplied by the the number of particles per volume $n\equiv N/V$ .

dn=nP(v){\rm d}v\,\frac{{\rm d}\Omega}{4\pi}

(1.74)

Consider a hole of area $\mathcal{A}$ on the wall of a container containing the gas (see Fig. 1.3). The flux through the hole is defined as

\Phi\equiv\frac{1}{\mathcal{A}}\frac{dN_{\rm cross}}{dt}\equiv\mbox{number of % particles crossing the hole per area per second}

(1.75)

From tube geometry in Fig. 1.3,

Figure 1.3: In each $d t$ a volume $\mathcal{A}h=\mathcal{A}vdt\cos\theta$ passes through the hole

the number of particles flying through the area $\mathcal{A}$ in time $d t$ with speed in $[v,v+{\rm d}v]$ and angles in $[\theta,\theta+{\rm d}\theta]$ and $[\phi,\phi+{\rm d}\phi]$ is $dN_{\rm cross}=dn\,\mathcal{A}h$ , where $\mathcal{A}h$ is the volume of the tube and $h=vdt\cos\theta$ is the height of the tube. Dividing by $\mathcal{A}$ and $d t$ we find the differential flux:

{\rm d}\Phi=nP(v)v\cos\theta{\rm d}v\,\frac{{\rm d}\Omega}{4\pi}\,.

(1.76)

${\rm d}\Phi$ is the number of particles passing through the hole per area per second with speed in $[v,v+{\rm d}v]$ and angles in $[\theta,\theta+{\rm d}\theta]$ and $[\phi,\phi+{\rm d}\phi]$ .

We can integrate the flux ${\rm d}\Phi$ over the velocity and over half of the sphere to find the total flux. Writing the $4\pi$ in the ${\rm d}\Omega/4\pi$ as $2\cdot 2\pi$ (see homework for motivation), we find:

	$\displaystyle\Phi=\int{\rm d}\Phi=n\int_{0}^{\infty}dvP(v)v\int_{0}^{\pi/2}% \frac{1}{2}\sin\theta\cos\theta d\theta\int_{0}^{2\pi}\frac{d\phi}{2\pi}\,\ =$	$\displaystyle\frac{1}{4}n\left\langle v\right\rangle$		(1.77)
	$\displaystyle=$	$\displaystyle n\sqrt{\frac{{kT}}{2\pi m}}$		(1.78)

We discussed an application or two of Eq. (1.77)

The pressure exerted by the atoms is found by calculating how many particles bounce of the wall per area per time, and the momentum the transfer they impart to the wall. A particle striking the wall velocity ${\bm{v}}_{i}=(v_{x},v_{y})$ , bounces off the wall with velocity ${\bm{v}}_{f}=(-v_{x},v_{y})$ delivering an impulse (see Fig. 1.4).

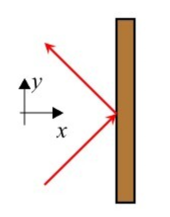
Figure 1.4: Momentum transfer to the wall is

The momentum transfer (or impulse) to the wall by the atom is $\Delta{\bm{p}}=2mv_{x}\,\hat{\bm{\imath}}=2mv\cos\theta\,\hat{\bm{\imath}}$ . (The momentum transfer to the atom by the wall is $\Delta{\bm{p}}={\bm{p}}_{f}-{\bm{p}}_{i}=-2mv_{x}\,\hat{\bm{\imath}}$ .) Recall that force is $F=\Delta p/\Delta t$ . The momentum transfer per area per per time, or force per area, created by the atoms with speed and angles in the ranges $[v,v+{\rm d}v]$ , $[\theta,\theta+{\rm d}\theta]$ , $[\phi,\phi+{\rm d}\phi]$ is

\frac{dF_{x}}{\mathcal{A}}=\Delta p_{x}\,{\rm d}\Phi={\rm d}\Phi\,(2mv\cos\theta)

(1.79)

Integrating over $v,\theta,\phi$ as in Eq. (1.77) gives the force per area or pressure. Of course this should give the ideal gas law $p=n{k_{\scriptscriptstyle B}T}$ . Computing the pressure is a matter of integration

p=\frac{F_{x}}{\mathcal{A}}=\int{\rm d}\Phi\,(2mv\cos\theta)=n{k_{% \scriptscriptstyle B}T}

(1.80)

Using ${\rm d}\Phi$ the details are similar to Eq. (1.77)

	$\displaystyle p=2nm\int_{0}^{\infty}dvP(v)v^{2}\int_{0}^{\pi/2}\frac{1}{2}\sin% \theta\cos^{2}\theta d\theta\int_{0}^{2\pi}\frac{d\phi}{2\pi}\,\ =$	$\displaystyle\frac{1}{3}n\left\langle mv^{2}\right\rangle$		(1.81)
	$\displaystyle=$	$\displaystyle n{k_{\scriptscriptstyle B}T}$		(1.82)

It is satisfying how the molecular theory of gasses reproduces the ideal gas law $p=n{k_{\scriptscriptstyle B}T}$ .